Euler’s Factoring Problem

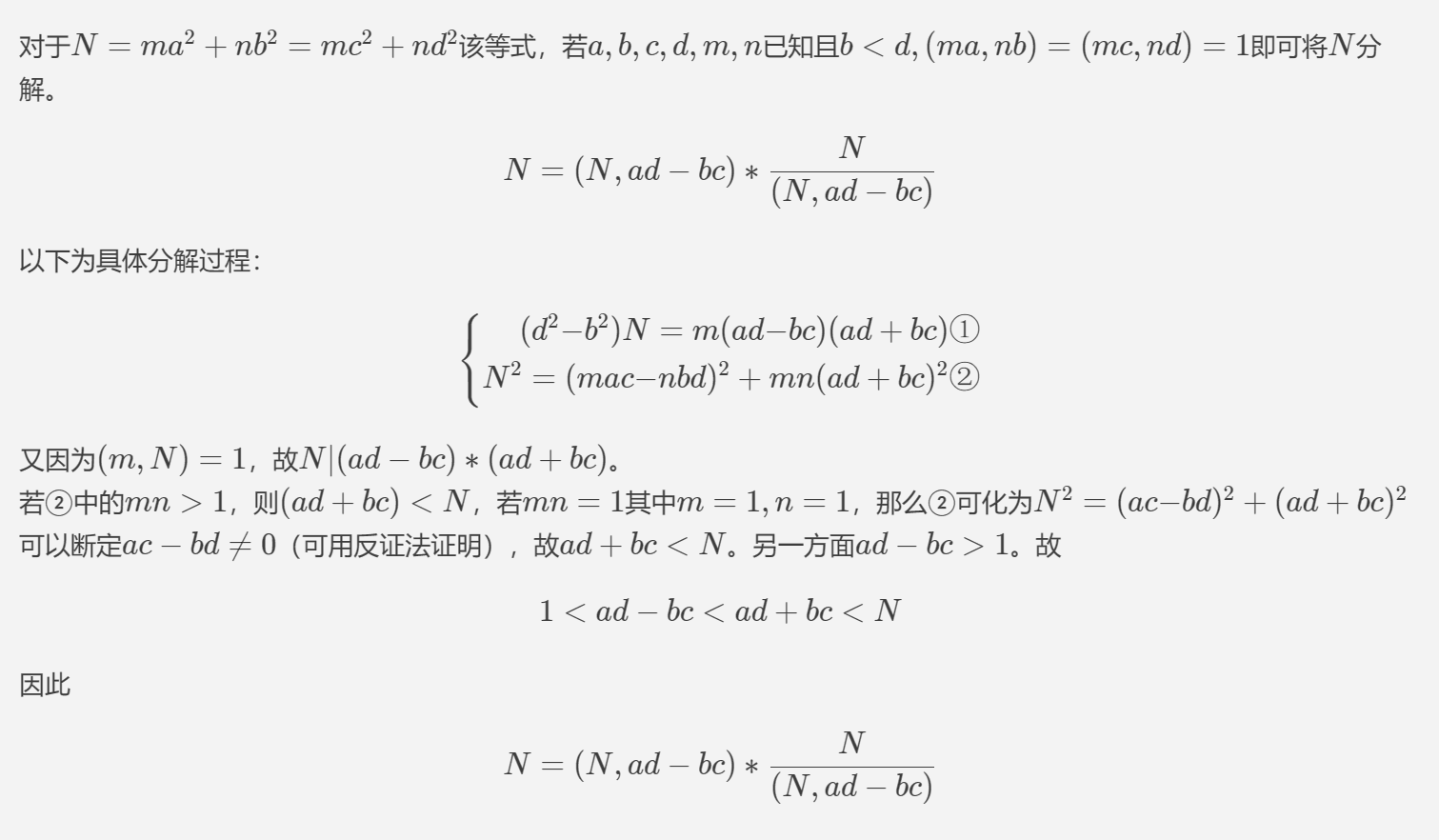
[NSSRound#11 Basic]ez_fac

from Crypto.Util.number import *  
import random  
from secret import flag,a0,a1,b0,b1  
  
p = getPrime(512)  
q = getPrime(512)  
e = getPrime(128)  
n = p*q  
assert pow(a0,2) + e * pow(b0,2) == n  
assert pow(a1,2) + e * pow(b1,2) == n  
m = bytes_to_long(flag)  
c = pow(m,e,n)  
  
print("c=",c)  
print("n=",n)  
print("a0=",a0)  
print("a1=",a1)  
print("b0=",b0)  
print("b1=",b1)

交互即可得到如上数据，在根据欧拉分解即可求解。

我的解答

from gmpy2 import *  
from Crypto.Util.number import *  
  
c= 11823688965873568224387587507940479280514052056216420023426097712900931724403427890713107717428719905417535431203211449891826321500281914443831186468829359837291903440583370816400179461641969321817527833377614790775093723861046323214230746507473615124667523158480111829343773605398115418127498898684103350326  
n= 66174334565820866135333027678221053466333802950685583680791384709232170906230028086032128773206750742475113443421594033367010911663734556976403332854215562495034650501672148398666048969273894940573751579464218934657554477490738909060195483243671784896096318342726887331933424091504584583549536005886378543317  
a0= 8134760879449430143239188880719185561738219028925333010419046822217672263260033279141972882169234707754692389970196313125592671017105020653394406795717247  
a1= 8134760879449430143239188714448245808726640875591381678937974571818448405741766588105154012463966515061676987093094590345453583569630982185618531416759777  
b0= 20138483781668396879412423684163519175255407889756657012434574713398820283243984339753137265206780130651728302960448651598  
b1= 93554898983019461516591670456408267226871638060548278467812159963007019501914788273724655962025719446735556508830366206338  
  
p=gcd(n,a0*b1-a1*b0)  
assert n%p==0  
q=n//p  
phi=(p-1)*(q-1)  
e=(a1**2-a0**2)//(b0**2-b1**2)  
d=invert(e,phi)  
m=pow(c,d,n)  
print(long_to_bytes(m))